Publications

2025

1. arXiv

   

   Procrustes Problems on Random Matrices

   Hajg Jasa, Ronny Bergmann, Christian Kümmerle, Avanti Athreya, and Zachary Lubberts

   Oct 2025

   Abs arXiv Bib

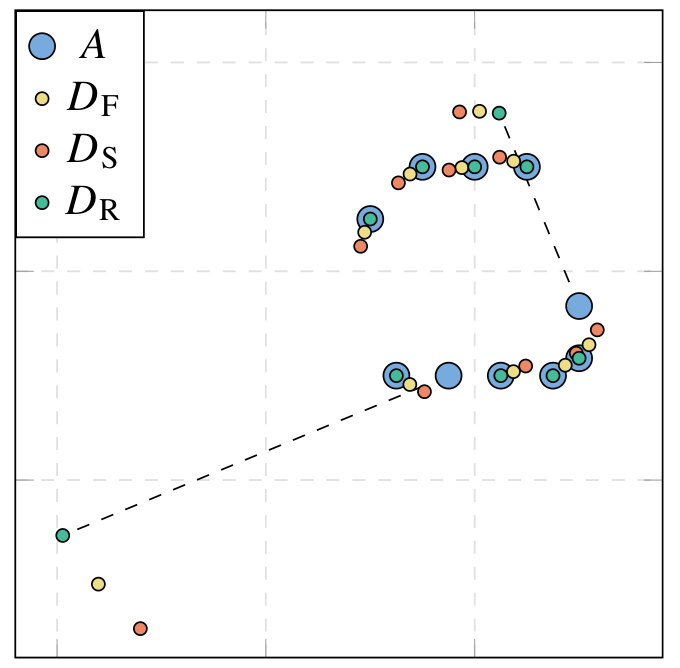
   Meaningful comparison between sets of observations often necessitates alignment or registration between them, and the resulting optimization problems range in complexity from those admitting simple closed-form solutions to those requiring advanced and novel techniques. We compare different Procrustes problems in which we align two sets of points after various perturbations by minimizing the norm of the difference between one matrix and an orthogonal transformation of the other. The minimization problem depends significantly on the choice of matrix norm; we highlight recent developments in nonsmooth Riemannian optimization and characterize which choices of norm work best for each perturbation. We show that in several applications, from low-dimensional alignments to hypothesis testing for random networks, when Procrustes alignment with the spectral or robust norm is the appropriate choice, it is often feasible to replace the computationally more expensive spectral and robust minimizers with their closed-form Frobenius-norm counterpart. Our work reinforces the synergy between optimization, geometry, and statistics.

   @online{AthreyaBergmannJasaKummerleLubberts:2025:1,
     author = {Jasa, Hajg and Bergmann, Ronny and K\"ummerle, Christian and Athreya, Avanti and Lubberts, Zachary},
     title = {Procrustes Problems on Random Matrices},
     month = oct,
     year = {2025},
   }

2. Zenodo

   ManoptExamples.jl

   Ronny Bergmann and Hajg Jasa

   Oct 2025

   DOI Bib

   @software{BergmannJasa:2025:17277311,
     author = {Bergmann, Ronny and Jasa, Hajg},
     title = {ManoptExamples.jl},
     month = oct,
     year = {2025},
     publisher = {Zenodo},
     version = {v0.1.16},
     doi = {10.5281/zenodo.17277311},
   }

3. arXiv

   

   The Intrinsic Riemannian Proximal Gradient Method for Convex Optimization

   Ronny Bergmann, Hajg Jasa, Paula John, and Max Pfeffer

   Jul 2025

   Abs arXiv Bib

   We consider a class of (possibly strongly) geodesically convex optimization problems on Hadamard manifolds, where the objective function splits into the sum of a smooth and a possibly nonsmooth function. We introduce an intrinsic convex Riemannian proximal gradient (CRPG) method that employs the manifold proximal map for the nonsmooth step, without operating in the embedding or tangent space. A sublinear convergence rate for convex problems and a linear convergence rate for strongly convex problems is established , and we derive fundamental proximal gradient inequalities that generalize the Euclidean case. Our numerical experiments on hyperbolic spaces and manifolds of symmetric positive definite matrices demonstrate substantial computational advantages over existing methods.

   @online{BergmansnJasaJohnPfeffer:2025:2,
     author = {Bergmann, Ronny and Jasa, Hajg and John, Paula and Pfeffer, Max},
     title = {The Intrinsic Riemannian Proximal Gradient Method for Convex
                Optimization},
     month = jul,
     year = {2025},
   }

4. arXiv

   

   The Intrinsic Riemannian Proximal Gradient Method for Nonconvex Optimization

   Ronny Bergmann, Hajg Jasa, Paula John, and Max Pfeffer

   Jun 2025

   Abs arXiv Bib

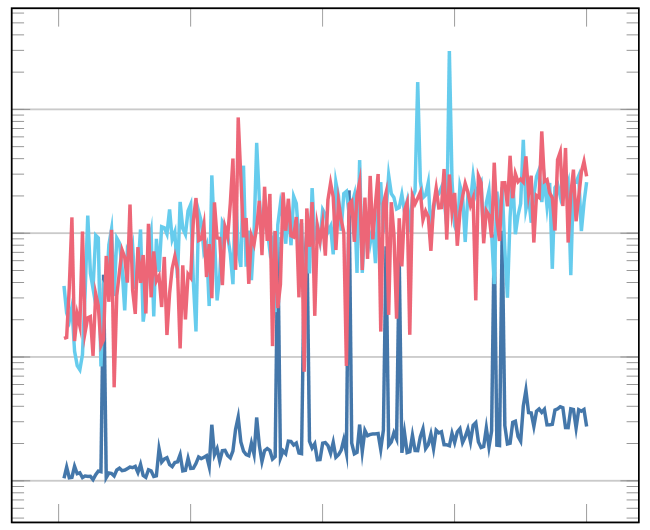
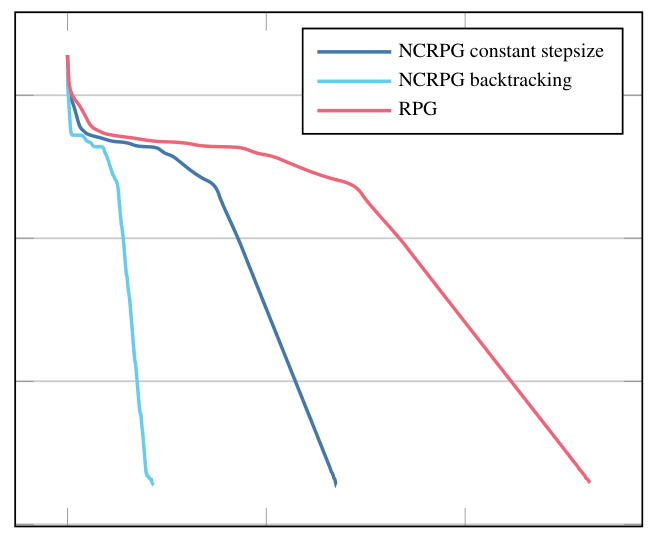
   We consider the proximal gradient method on Riemannian manifolds for functions that are possibly not geodesically convex. Starting from the forward-backward-splitting, we define an intrinsic variant of the proximal gradient method that uses proximal maps defined on the manifold and therefore does not require or work in the embedding. We investigate its convergence properties and illustrate its numerical performance, particularly for nonconvex or nonembedded problems that are hence out of reach for other methods.

   @online{BergmannJasaJohnPfeffer:2025:1,
     author = {Bergmann, Ronny and Jasa, Hajg and John, Paula and Pfeffer, Max},
     title = {The Intrinsic Riemannian Proximal Gradient Method for Nonconvex
                Optimization},
     month = jun,
     year = {2025},
   }

2024

1. arXiv

   

   The Riemannian Convex Bundle Method

   Ronny Bergmann, Roland Herzog, and Hajg Jasa

   Feb 2024

   Abs arXiv Bib

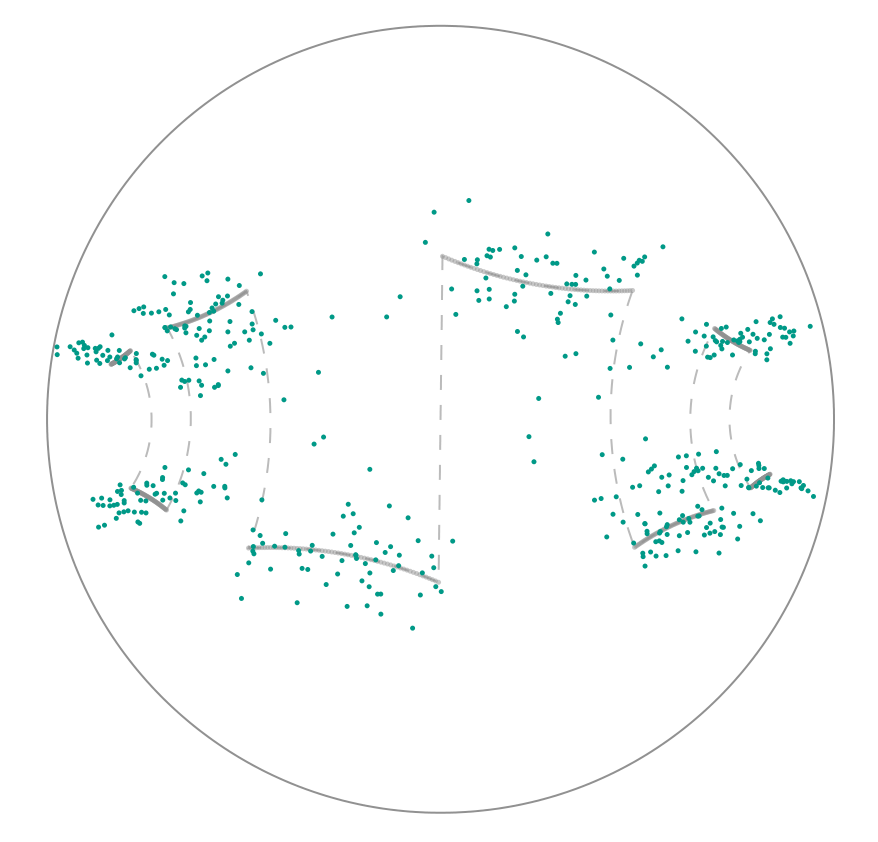
   We introduce the convex bundle method to solve convex, non-smooth optimization problems on Riemannian manifolds of bounded sectional curvature. Each step of our method is based on a model that involves the convex hull of previously collected subgradients, parallelly transported into the current serious iterate. This approach generalizes the dual form of classical bundle subproblems in Euclidean space. We prove that, under mild conditions, the convex bundle method converges to a minimizer. Several numerical examples implemented using Manopt.jl illustrate the performance of the proposed method and compare it to the subgradient method, the cyclic proximal point algorithm, as well as the proximal bundle method.

   @online{BergmannHerzogJasa:2024:1,
     author = {Bergmann, Ronny and Herzog, Roland and Jasa, Hajg},
     month = feb,
     year = {2024},
     title = {The Riemannian Convex Bundle Method},
   }